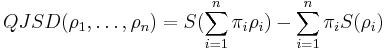Jensen–Shannon divergence
In probability theory and statistics, the Jensen–Shannon divergence is a popular method of measuring the similarity between two probability distributions. It is also known as information radius (IRad)[1] or total divergence to the average.[2] It is based on the Kullback–Leibler divergence, with the notable (and useful) difference that it is always a finite value. The square root of the Jensen–Shannon divergence is a metric.[3][4]
Contents |
Definition
Consider the set 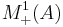 of probability distributions where A is a set provided with some σ-algebra of measurable subsets. In particular we can take A to be a finite or countable set with all subsets being measurable.
of probability distributions where A is a set provided with some σ-algebra of measurable subsets. In particular we can take A to be a finite or countable set with all subsets being measurable.
The Jensen–Shannon divergence (JSD) 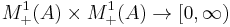 is a symmetrized and smoothed version of the Kullback–Leibler divergence
is a symmetrized and smoothed version of the Kullback–Leibler divergence 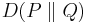 . It is defined by
. It is defined by
where 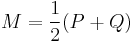
If A is countable, a more general definition, allowing for the comparison of more than two distributions, is:
where 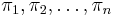 are the weights for the probability distributions
are the weights for the probability distributions 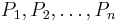 and
and 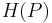 is the Shannon entropy for distribution
is the Shannon entropy for distribution  . For the two-distribution case described above,
. For the two-distribution case described above,
Bounds
According to Lin (1991), the Jensen–Shannon divergence is bounded by 1.
Relation to mutual information
Jensen-Shannon divergence is the mutual information between a random variable  from a mixture distribution
from a mixture distribution 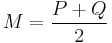 and a binary indicator variable
and a binary indicator variable  where
where 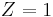 if
if  is from
is from  and
and 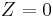 if
if  is from
is from  .
.
It follows from the above result that Jensen-Shannon divergence is bounded by 0 and 1 because mutual information is non-negative and bounded by 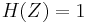 .
.
One can apply the same principle to the joint and product of marginal distribution (in analogy to Kullback-Leibler divergence and mutual information) and to measure how reliably one can decide if a given response comes from the joint distribution or the product distribution—given that these are the only possibilities.[5]
Quantum Jensen-Shannon divergence
The generalization of probability distributions on density matrices allows to define quantum Jensen–Shannon divergence (QJSD).[6][7] It is defined for a set of density matrices 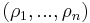 and probability distribution
and probability distribution 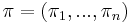 as
as
where 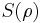 is the von Neumann entropy. This quantity was introduced in quantum information theory, where it is called the Holevo information: it gives the upper bound for amount of classical information encoded by the quantum states
is the von Neumann entropy. This quantity was introduced in quantum information theory, where it is called the Holevo information: it gives the upper bound for amount of classical information encoded by the quantum states 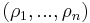 under the prior distribution
under the prior distribution  (see Holevo's theorem) [8] Quantum Jensen–Shannon divergence for
(see Holevo's theorem) [8] Quantum Jensen–Shannon divergence for 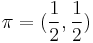 and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states [9] but it is unknown whether the metric property holds in general.[7]
and two density matrices is a symmetric function, everywhere defined, bounded and equal to zero only if two density matrices are the same. It is a square of a metric for pure states [9] but it is unknown whether the metric property holds in general.[7]
Applications
For an application of the Jensen-Shannon Divergence in Bioinformatics and Genomic comparison see (Sims et al., 2009; Itzkovitz et al. 2010) and in protein surface comparison see (Ofran and Rost, 2003).
Notes
- ^ Hinrich Schütze; Christopher D. Manning (1999). Foundations of Statistical Natural Language Processing. Cambridge, Mass: MIT Press. p. 304. ISBN 0-262-13360-1. http://nlp.stanford.edu/fsnlp/.
- ^ Dagan, Ido; Lillian Lee, Fernando Pereira (1997). "Similarity-Based Methods For Word Sense Disambiguation". Proceedings of the Thirty-Fifth Annual Meeting of the Association for Computational Linguistics and Eighth Conference of the European Chapter of the Association for Computational Linguistics: pp. 56–63. http://citeseer.ist.psu.edu/dagan97similaritybased.html. Retrieved 2008-03-09.
- ^ Endres, D. M.; J. E. Schindelin (2003). "A new metric for probability distributions". IEEE Trans. Inf. Theory 49 (7): pp. 1858–1860. doi:10.1109/TIT.2003.813506.
- ^ Ôsterreicher, F.; I. Vajda (2003). "A new class of metric divergences on probability spaces and its statistical applications". Ann. Inst. Statist. Math. 55 (3): pp. 639–653. doi:10.1007/BF02517812.
- ^ Schneidman, Elad; Bialek, W; Berry, M.J. 2nd (2003). "Synergy, Redundancy, and Independence in Population Codes". Journal of Neuroscience 23 (37): 11539–11553. PMID 14684857.
- ^ A. P. Majtey, P. W. Lamberti, and D. P. Prato, Jensen-Shannon divergence as a measure of distinguishability between mixed quantum states, Phys. Rev. A 72, 052310 (2005)
- ^ a b J. Briet, P. Harremoes, Properties of classical and quantum Jensen-Shannon divergence
- ^ A.S.Holevo, Bounds for the quantity of information transmitted by a quantum communication channel, Problemy Peredachi Informatsii 9, 3-11 (1973) (in Russian) (English translation: Probl. Inf. Transm., 9, 177-183 (1975)))
- ^ S. L. Braunstein, C. M. Caves, Phys. Rev. Lett. 72 3439 (1994)
References
- Jensen-Shannon Divergence and Hilbert space embedding, Bent Fuglede and Flemming Topsøe University of Copenhagen, Department of Mathematics [1]
- Lin, J. (1991). "Divergence measures based on the shannon entropy". IEEE Transactions on Information Theory 37 (1): 145–151. doi:10.1109/18.61115. https://www.cise.ufl.edu/~anand/sp06/jensen-shannon.pdf.
- A family of statistical symmetric divergences based on Jensen's inequality, F. Nielsen [2]
- Y. Ofran & B. Rost. Analysing Six Types of Protein-Protein Interfaces. J. Mol. Biol., 325: 377—387, 2003.
- G.E. Sims, S.R. Jun, G. Wu. & S.H. Kim Alignment-free genome comparison with feature frequency profiles (FFP) and optimal resolutions. Proc. Natl. Acad. Sci. USA. 106(8):2677-82
- S. Itzkovitz, E. Hodis, E. Segal, "Overlapping codes within protein-coding sequences," Genome Res., November 2010, 20:1582-1589
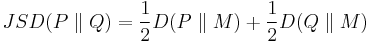
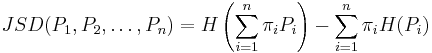
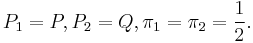
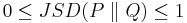
![\begin{align}
I(X; Z) &= H(X) - H(X|Z)\\
&= -\sum M \log M %2B \frac{1}{2} \left[ \sum P \log P %2B \sum Q \log Q \right] \\
&= -\sum \frac{P}{2} \log M - \sum \frac{Q}{2} \log M %2B \frac{1}{2} \left[ \sum P \log P %2B \sum Q \log Q \right] \\
&= \frac{1}{2} \sum P \left( \log P - \log M\right ) %2B \frac{1}{2} \sum Q \left( \log Q - \log M \right) \\
&= JSD(P \parallel Q)
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/f45702e51681515c424c0ed2ba489ad7.png)